Attività da proporre ai bambini!
Abbiamo disegnato e, anziché colorare gli spazi del nostro disegno riempiendoli di vari colori, abbiamo usato i punti, poi le linee per creare l'effetto del colore!
giovedì
Un grande architetto: Antonio Sant'Elia
« Le case dureranno meno di noi. Ogni generazione dovrà fabbricarsi la sua città. Questo costante rinnovamento dell'ambiente architettonico contribuirà alla vittoria del Futurismo. »
Antonio Sant'Elia (Como, 30 aprile 1888 – Monte Hermada, 10 ottobre 1916) è stato un architetto italiano, appartenente al futurismo.
Geometria e arte: la prospettiva!
La prospettiva è un insieme di proposizioni e di procedimenti di carattere geometrico-matematico che consentono di costruire l'immagine di una figura dello spazio su un piano, proiettando la stessa da un centro di proiezione posto a distanza finita.
Si tratta quindi di una proiezione centrale, o conica. La specificazione è utile per distinguerla dalla prospettiva parallela, modo alternativo, anche se non di uso corrente, di chiamare le assonometrie. La parziale comunanza dei termini è dovuta al fatto che l'assonometria, per motivi strutturali legati alla determinazione dell'immagine su un solo piano, può essere vista come un caso particolare della prospettiva, quando il centro di proiezione, anziché essere un punto proprio, è all'infinito.
Si tratta quindi di una proiezione centrale, o conica. La specificazione è utile per distinguerla dalla prospettiva parallela, modo alternativo, anche se non di uso corrente, di chiamare le assonometrie. La parziale comunanza dei termini è dovuta al fatto che l'assonometria, per motivi strutturali legati alla determinazione dell'immagine su un solo piano, può essere vista come un caso particolare della prospettiva, quando il centro di proiezione, anziché essere un punto proprio, è all'infinito.
La geometria proiettiva!
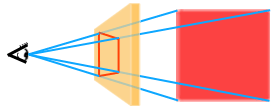
La geometria proiettiva nasce come strumento legato al disegno in prospettiva, e viene formalizzata nel XIX secolo come un arricchimento della geometria cartesiana. La geometria proiettiva include i "punti all'infinito" ed elimina quindi alcune casistiche considerate fastidiose, come la presenza di rette parallele.
In questa geometria molte situazioni si semplificano: due piani distinti si intersecano sempre in una retta, e oggetti differenti della geometria analitica (come le coniche ellisse, parabola e iperbole) risultano essere equivalenti in questo nuovo contesto.
La geometria proiettiva è anche un esempio di compattificazione: similmente a quanto accade con la proiezione stereografica, aggiungendo i punti all'infinito lo spazio diventa compatto, cioè "limitato", "finito".
In questa geometria molte situazioni si semplificano: due piani distinti si intersecano sempre in una retta, e oggetti differenti della geometria analitica (come le coniche ellisse, parabola e iperbole) risultano essere equivalenti in questo nuovo contesto.
La geometria proiettiva è anche un esempio di compattificazione: similmente a quanto accade con la proiezione stereografica, aggiungendo i punti all'infinito lo spazio diventa compatto, cioè "limitato", "finito".
La geometria piana si occupa delle figure geometriche nel piano. A partire dal concetto primitivo di retta, vengono costruiti i segmenti, e quindi i poligoni come il triangolo, il quadrato, il pentagono, l'esagono, ecc..
Le quantità numeriche importanti nella geometria piana sono la lunghezza, l'angolo e l'area. Ogni segmento ha una lunghezza, e due segmenti che si incontrano in un estremo formano un angolo. Ogni poligono ha un'area. Molti teoremi della geometria piana mettono in relazione le lunghezze, angoli e aree presenti in alcune figure geometriche. Ad esempio, la somma degli angoli interni di un triangolo risulta essere un angolo piatto, e l'area di un rettangolo si esprime come prodotto delle lunghezze dei segmenti di base e altezza. La trigonometria studia le relazioni fra gli angoli e le lunghezze.
Le quantità numeriche importanti nella geometria piana sono la lunghezza, l'angolo e l'area. Ogni segmento ha una lunghezza, e due segmenti che si incontrano in un estremo formano un angolo. Ogni poligono ha un'area. Molti teoremi della geometria piana mettono in relazione le lunghezze, angoli e aree presenti in alcune figure geometriche. Ad esempio, la somma degli angoli interni di un triangolo risulta essere un angolo piatto, e l'area di un rettangolo si esprime come prodotto delle lunghezze dei segmenti di base e altezza. La trigonometria studia le relazioni fra gli angoli e le lunghezze.
La Geometria Euclidea
La geometria coincide fino all'inizio del XIX secolo con la geometria euclidea. Questa definisce come concetti primitivi il punto, la retta e il piano, e assume la veridicità di alcuni assiomi, gli Assiomi di Euclide. Da questi assiomi vengono quindi dedotti dei teoremi anche complessi, come il Teorema di Pitagora ed i teoremi della geometria proiettiva.
La scelta dei concetti primitivi e degli assiomi è motivata dal desiderio di rappresentare la realtà, e in particolare gli oggetti nello spazio tridimensionale in cui viviamo. Concetti primitivi come la retta ed il piano vengono descritti informalmente come "fili e fogli di carta senza spessore", e d'altro canto molti oggetti della vita reale vengono idealizzati tramite enti geometrici come il triangolo o la piramide. In questo modo, i teoremi forniscono fin dall'antichità degli strumenti utili per le discipline che riguardano lo spazio in cui viviamo: meccanica, architettura, geografia, navigazione, astronomia.
La scelta dei concetti primitivi e degli assiomi è motivata dal desiderio di rappresentare la realtà, e in particolare gli oggetti nello spazio tridimensionale in cui viviamo. Concetti primitivi come la retta ed il piano vengono descritti informalmente come "fili e fogli di carta senza spessore", e d'altro canto molti oggetti della vita reale vengono idealizzati tramite enti geometrici come il triangolo o la piramide. In questo modo, i teoremi forniscono fin dall'antichità degli strumenti utili per le discipline che riguardano lo spazio in cui viviamo: meccanica, architettura, geografia, navigazione, astronomia.
La GEOMETRIA!!!
La geometria (dal greco antico γεωμετρία, composto da γεω, geo = "terra" e μετρία, metria = "misura", tradotto quindi letteralmente come misurazione della terra) è quella parte della scienza matematica che si occupa delle forme nel piano e nello spazio e delle loro mutue relazioni.
Iscriviti a:
Post (Atom)